By talking to a few hundred senators Cicero was able to start a war. Luther has done it by nailing a piece of paper to a door and Hearst with a journal with maybe 100000 readers. Radio and television have been considered big revolutions in opinion forming. It is thus reasonable to wonder if the changes caused by social media are something new, different from the past. On the one hand the past shows a more or less gradual increase in the speed and strength of information dissemination and opinion-forming. The present follows this quantitative rule but, on the other hand, it could also be qualitatively different.

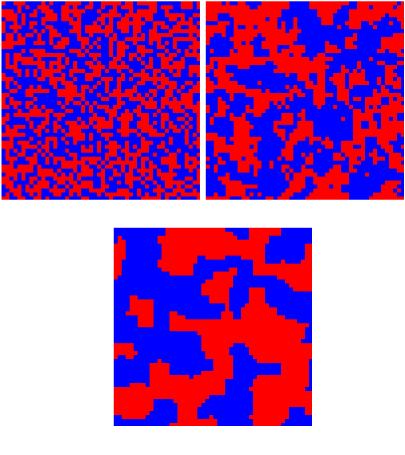
There are many models for opinion-forming (rumor-spreading) but the one I like most is based on the well-known Ising model. See for example Ising model of rumour spreading in interacting communities, by Ostili et al. The model is simple: the distribution of beliefs of a population choosing between two opinions \(O=1\) and \(O=-1\) is modeled by minimization dynamics of an energy function

\[E=-J \sum_i \sum_{j\in N_i} O_i O_j.\]

This formula models a tendency of people to adopt similar opinions with those they are in contact with (their neighborhood). If the neighbourhood \(N_i\) is small the population contains many small communities of like opinion. But beyond a certain size of neighborhoods one can have situations in which there is only a small number of communities and everyone in the same community has the same opinion. Moreover the transition can be sudden.

Ising agents with three increasing neighborhood sizes (interaction strengths)

A conclusion of such an analysis would be that, assuming the neighborhood size has increased constantly in the past, it is possible that the opinion forming dynamics have changes drastically at a certain point in time, probably quite recently. At this point many measurable variables could have drastically changed. For example the average number of people one knows (talks to) having a different opinion would drop to almost zero. We do not really know if this is the case and it is difficult to go back in time and measure.

A similar physically inspired model of social dynamics is beautifully presented as a
Parable of the Polygons .