Can WORDLE be always solved?
In the past months the Twitter has been overtaken by stacks of colored boxes. It is the fault of a new words-game: WORDLE. Free and with a minimalistic design the game has received a well deserved attention.
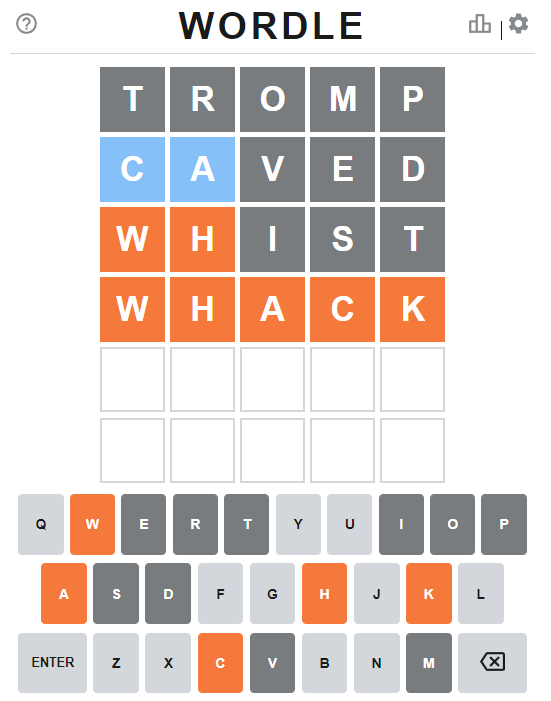
Each day a five letters word is proposed and you have six tries to guess it. For each guess the letters that in your guess which can be found in the solution are highlighted (orange for letters found in the same position and blue if not).
By now one can find quite a few articles discussing winning strategies and even web apps offering word suggestions for the game. Given the apparent simplicity of the game I want a more exact answer to simple questions: can the game be solved for any proposed solution word? which is the best starting word? The short answer is yes, there is a strategy to always find the answer in six words and less. And my best starting word is LATEN.
Let us start with properly setting up the game. One starts with a list (L) of possible guesses. For the original game this list contains 12972 five letters words, some of them quite obscure. The solutions are chosen from a smaller sublist list (A) of 2315 more common words. We suppose the choice to be uniformly random. The goal is to always find the solution using less than six guesses. If the solution can always be found we want to minimize the average number of guesses.
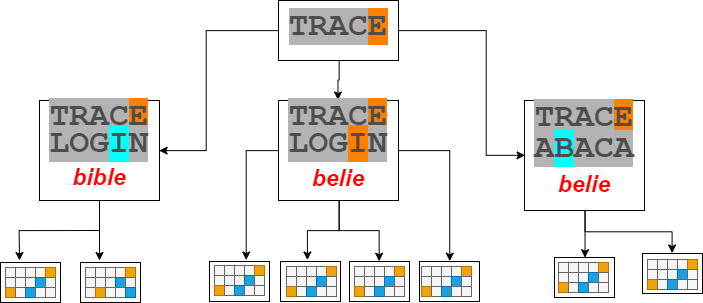
The game is defined by a directed graph where each node is a possible color configuration. The children of each node are the color configurations that can be obtained by adding another guess, for each possible guess and each possible solution compatible with the node. Let us suppose that we start with the word TRACE and the solution is either BELIE or BIBLE. A portion of the game tree would look like this:
The actual root of the tree is the empty configuration with 12972 x 2315 children on the first level. An important feature of each node (configuration) \(C\) is the set \(S(C)\) of solutions compatible with it. If this set contains only one solution, we can “guess” it at the next step and the game ends. The tree has therefore five levels and the leaves are of two types:
- nodes with only one compatible solution. They correspond to a correct guess at the next step.
- nodes with more than one compatible solution on the fifth level. They correspond to a (possible) loss.
With each node we can associate a minimal average number of extra guesses needed to win, starting from that node, let us call it \(g(C)\). Each leaf of type one has by definition \(g(C)=1\) and each leaf of type two has \(g(C)=g_{loss}\) where \(g_{loss}\) is some big number. One can thus derive a master equation:
\[g(C) =1+MIN_{All\, guesses,\, w} \left( \frac{\sum_{All\, solutions\, in\, S(C),\, s} g(C_{s,w})}{|S(C)|} \right)\]where \(C_{s,w}\) is the child of the node (configuration) \(C\) obtained by adding the guess \(w\) when the solution is \(s\). This is a mathematical form of the intuition that the number of guesses still needed to solve the game if starting at node \(C\) is one unit larger than what is needed starting from the best configuration that can be reached in one step from \(C\), averaged over all the possible solutions.
Once solved, the master equation can answer all our questions and also provides the perfect strategy at every step. The game can always be solved in less than six steps if and only if the solution of the master equation is independent of \(g_{loss}\). Then the child of the root with the highest average \(g\) provides the perfect guess. The value of \(g\) at the root is the average number of guesses from the start of the game until the solution is found. Unfortunately the full tree is quite big and very difficult to solve on my system, therefore a few shortcuts are needed.
First I use the observation that if one inputs the words TROMP, RUGBY, FLANK, WHIST and CAVED, the resulting configuration is unique for most possible solutions (thus providing the correct guess at the last step). Unfortunately there remain 13 pairs of solutions that cannot be thus distinguished, like MELON and LEMON or BIBLE and BELIE. The search is ongoing, as the existence of a quintuple of words with unique configurations for each solution is a sufficient (but not necessary) condition for the game to be solvable for any solution.
Inspired by this, one can restrict the list of possible guesses. Obviously a game where not all words are allowed would provide a bound for the best strategy. Indeed, using only the 9 words LATEN, CRISP, DOUGH, WOMBY, FLAKS, SERVE, RIGOL, BLOND, and TESTY as guesses one can always solve WORDLE in 3.9 steps in average. Check out a text solver here. The very best strategy probably needs many more words for the guesses but then the game tree gets too big. Next step would be to use the same approach for the Hard Mode of the game. Because in that mode any “hints must be used in subsequent guesses” the game-tree should be much smaller, as many combinations of guesses are not allowed.
UPDATE. I found a smaller set of guesses that can solve for all 2315 solutions with
only 8 guesses:
ANTED,
CRISP, WOMBY, FLAKS, RIGOL,
LOUGH,
LURVE,
THOFT, starting with ANTED. In average the
best strategy with these words takes 3.92 steps.